Lesson 17: Modes - The Parallel Approach

You may recall in Lesson 13 how I explained how 6 modes (Dorian, Phrygian, etc.) can be derived from a major scale, and how we call this way of thinking the derivative approach.

In short, the derivative approach shows us how a group (or set) of modes exist within the same parent scale.

In this lesson we approach the same subject of modes but from a different perspective called the parallel approach, which shows us how we can alter a parent scale directly to create any one of the major scale modes we want, with the same root as that parent scale. And that's a key concept here... both scales will have the same root. In fact that's what the word "parallel" means... two scales or keys that have the same root are said to be parallel scales or keys. However, before I get into all of the gory details, let's explore the parent scale concept further.

There are 3 main parent scales in Western music. They are:

1. the major scale
2. the melodic minor scale
3. the harmonic minor scale

These 3 scales are called parent scales because many other important scales can be derived from them; it's just a matter of shifting our "root perspective" through each scale degree of the parent scale to find each derivative (or relative) mode. We've already seen how this works with the major scale, but this concept can also be applied to the other parent scales: melodic and harmonic minor.

Now what's cool about this is: when you learn how to play a parent scale on the guitar in its various positions across the neck, you are also learning the same patterns (or fingerings) for each mode related to that parent scale. Remember, each pattern can mean 7 different things. How cool is that?

Hopefully, this idea became clear to you in Lesson 13. In fact, that was the main point of that lesson, that all 7 patterns presented in Lesson 13 can be used in any of the 7 different modal contexts. For instance, if you're playing over an Fmaj.7 chord, any one of those (C major scale or natural note) patterns will sound like F Lydian. If this doesn't make sense to you, please revisit Lesson 13 and go through all of the playing exercises. It's important that you understand this concept before proceeding.

If you attend the Berklee College of Music as a first semester guitar student, one of the main things you have to learn is all of the major scale fingerings on the guitar in all 15 theoretical keys and know how those same patterns can be used in any of the relative modal contexts: Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian. This sounds like a lot of work, and it is, but it's an excellent starting point for really understanding scale theory on the fingerboard.

When you can think derivatively on the guitar and perform the calculus of shifting between modes and relative parent keys, you've really made progress. But, doing this with the major scale is really only the entry point. During your second semester you conquer the melodic minor scale (and its relative modes) and during your third semester you do the same thing yet again but the focus is on harmonic minor.

In total, after 3 semesters of work, you'll have uncovered 21 modes with these 3 parents scales. Wow, that's a lot of sonic territory! In this lesson, however, I'm going to limit our discussion to understanding the parallel approach using only a major scale. So, don't worry about the melodic or harmonic minor scales and their respective modes for now. We'll cover those topics in later lessons.

So, here we go!

As you will discover (if you haven't already) there are basically two kinds of modes: major sounding modes and minor sounding modes. Classifying the major scale modes in this way we get the following breakdown.

The major sounding modes:

• Ionian (the major scale - it is, indeed, a mode.)
• Lydian
• Mixolydian

The minor sounding modes:

• Dorian
• Phrygrian
• Aeolian (the natural minor scale)
• Locrian - Indeed Locrian is a mode, but it is rarely, if ever, used in a modal context - that is, musicians rarely jam in the mode or key of Locrian. It sounds too unstable and/or weird.

Please keep in mind that in many cases the word mode means the same thing as the word scale. Also keep in mind that the words mode and scale can be used as synonyms for the word key. The 3 terms basically all mean the same thing.

The parallel approach to modes can be summed up by asking yourself the following question:

1. How can we alter a parent scale to create the other modal scales with the same root?

Since this lesson only concerns itself with the major scale modes, we can ask a more specific question:

2. How can we alter a major scale to get the 6 parallel major scale modes (Dorian, Phrygian, ..., Locrian)?

For example, how can we alter a C major scale to get C Dorian, C Phrygian, C Lydian, C Mixolydian, C Aeolian, or C Locrian? Let's run through an example.

The Goal: Alter a C major scale to create a C Dorian scale.

The Answer: The answer comes down to learning the scale formulas for each mode. In fact, if you recall, I already gave you the formulas in Lesson 13 when I provided an intervallic analysis of each note in each mode relative to the key of C major. However, before I just repeat those formulas again, I first want to show you how you can derive them for yourself.

The Derivation:

1. First we'll take the derivative approach and figure out what Dorian scale is "hiding out" inside of C major.
   • At this point we should know the answer is D Dorian because D is the second note of a C major scale and starting any major scale at the second scale degree yields Dorian mode.
2. Then, we'll "move backwards" and compare D Dorian to its parallel major scale, D major.
   • The difference between these two scales should tell us how to alter a C major scale to produce C Dorian.
3. So, here we go!

We know the key of C major contains the following natural notes:

Note Function:	R	2	3	4	5	6	7	R
The C Major Scale:	C	D	E	F	G	A	B	C

We also know that if we start this scale at the 2nd scale degree we produce a D Dorian scale which contains the following notes:

Note Function:	R	2	b3	4	5	6	b7	R
The D Dorian Scale:	D	E	F	G	A	B	C	D

This is indeed the derivative approach as we derived Dorian mode from the major scale by shifting the root perspective, but let's go a little further with this idea. Let's compare D Dorian against its parallel major key, the D major scale, and see where they differ. Remember, parallel scales share the same root (or tonal center).

Note Function:	R	2	3	4	5	6	7	R
The D Major Scale:	D	E	F#	G	A	B	C#	D

The scales differ at the 3rd and 7th scale degrees. In D Dorian we have an F and C natural while in D major we have an F# and C#. This is where the insight lies. In order to create a Dorian scale from its parallel major scale, we need to lower the 3rd and 7th scale degrees of the major scale each by a half step.

In the case of a D major scale, if we lower the 3rd and 7th notes by a half step, we'll get a scale that has all natural notes, D Dorian.

Let's go back to the C major scale... How do we alter a C major scale to produce C Dorian? We lower the 3rd and 7th scale degrees by a half step.

Note Function:	R	2	3	4	5	6	7	R
The C Major Scale:	C	D	E	F	G	A	B	C

Note Function:	R	2	b3	4	5	6	b7	R
The C Dorian Scale:	C	D	Eb	F	G	A	Bb	C

At this point in the game, I hope you see that C Dorian has the same notes as a Bb major scale. And this should make sense because if we start a Bb major scale at the second scale degree, which is a C note, we'll get C Dorian.

Note Function:	R	2	3	4	5	6	7	R
The Bb Major Scale:	Bb	C	D	Eb	F	G	A	Bb

We've come full circle.

The above "method" uses both a combination of derivative and parallel thinking. As you can see, these two approaches are really looking at two sides of the same coin, and this is probably where most people get confused when they're first learning about this stuff. They don't yet know how to switch gears between these two types of thinking.

From my experience teaching, a student that gets confused about this stuff is not putting in the work. They still don't really understand intervals or major scale construction or the Circle of 5ths, etc. So, don't be like that. If this stuff is over your head, it's a good indication that you haven't really understood previous lessons. If this is the case, go back, start over and do the work. You need a better understanding of the fundamentals.

However, if this makes sense to you, then congratulations. Most of the hard work has been done. We're almost there.

Remember: This method is called the parallel approach because we compare two scales with the same root note to each other. In the case where C was the tonal center, we compared a C major scale against a C Dorian scale. In the case where D was the tonal center, we compared a D major scale against a D Dorian scale. This is the heart of the parallel method.

Repeat this process again to find the scale formula for a Phrygian scale. Simply compare E Phrygian to the E major scale and make note of the differences. If you continue along this line you can also compare F Lydian to an F major scale, G Mixolydian to a G major scale, A Aeolian to an A major scale, and finally, B Locrian to a B major scale. If you do this, you will "discover" all the scale formulas for all the major scale modes.

Dig?

The following chart illustrates the two different approaches to modes (derivative and parallel) using a C major scale. This diagram comes from page 14 of Mick Goodrick's book, The Advancing Guitarist.

Get Mick's book and read it too. It had a positive influence on my playing after reading it many years ago and helped me think in new and creative ways.

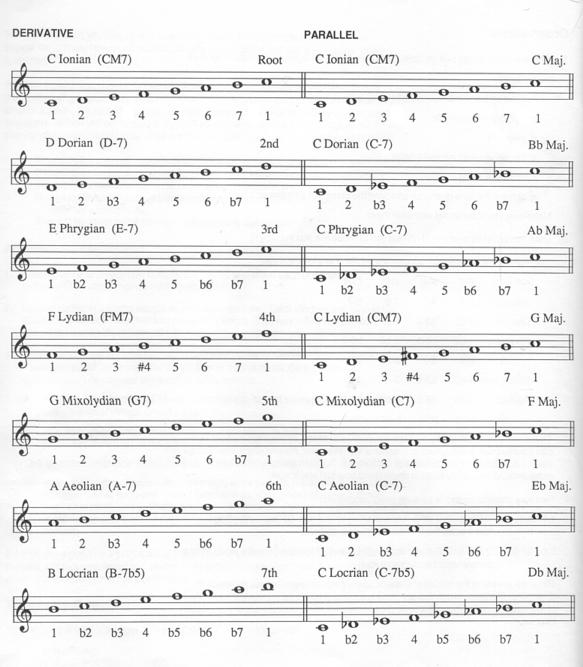
As the above chart illustrates, we get the following modal scale formulas:

Ionian:	R, 2, 3, 4, 5, 6, 7, R
Dorian:	R, 2, b3, 4, 5, 6, b7, R
Phrygian:	R, b2, b3, 4, 5, b6, b7, R
Lydian:	R, 2, 3, #4, 5, 6, 7, R
Mixolydian:	R, 2, 3, 4, 5, 6, b7, R
Aeolian:	R, 2, b3, 4, 5, b6, b7, R
Locrian:	R, b2, b3, 4, b5, b6, b7, R

Study this chart well. As with most of the charts I show you, you should commit them to memory or at least be able to derive them. For instance, you should know things like this: to make a Lydian scale, simply raise the 4th degree of a major scale by a half step. To make a Mixolydian scale, lower the 7th degree of a major scale by a half step, and so on.

So, understanding the parallel approach really comes down to learning and memorizing the modal scale formulas. But, again you should also understand how to derive these formulas which is better than just memorizing them.

To Recap: One Last Example:  Say you want to figure out the notes of a G Aeolian (Natural Minor) scale.

• First, use the parallel major scale, G major, as a reference point.
• G Major ==> G, A, B, C, D, E, F#, G
• Then apply the Aeolian scale formula to it ==> R, 2, b3, 4, 5, b6, b7, R
• As we can see from the formula, we'll need to flat the 3rd, 6th and 7th scale degrees of G major to get G Aeolian.
• The result ==> G, A, Bb, C, D, Eb, F, G
• Now check your work using the derivative approach. Which major scale has G as its 6th scale degree?
  • Why the 6th scale degree? Because starting any major scale at its 6th degree will produce an Aeolian (or Natural Minor) scale.
• The answer is Bb major. What's the key signature for Bb major?
• 2 flats: B flat and E flat. (Big Ed). Remember Big Ed and Donna?
• Wow, that's what we have above. We're done. Good work.

Now, I really haven't presented anything new in this lesson compared to Lesson 13, but I have showed you the same information in a different way. Both the derivative and parallel approaches have their advantages and disadvantages. The derivative approach seems to yield quicker results for the beginner while the parallel approach provides a deeper understanding of scale construction - we work directly with the language of intervals. One will naturally progress towards using the parallel approach in their playing and thinking if one hangs in there for the long haul. At least, that's what happened with me and my practice.

All I can say is that it's totally worth it. The amount of freedom attained from this knowledge is awesome. It's completely liberating and empowering. Because once you understand these concepts and learn how to apply them to your playing, you will have a language or map for the most common sounds heard in music. How cool is that?

A Playing Exercise: Use the low E string on your guitar as a pedal tone and improvise against it using all seven major scale modes. That is, for about 3 or 4 minutes at a time, improvise using:

• E Ionian (an E major scale)
• E Dorian (a D major scale)
• E Phrygian (a C major scale)
• E Lydian (a B major scale)
• E Mixolydian (an A major scale)
• E Aeolian (a G major scale)
• E Locrian (an F major scale)

Be sure to use a mixture of both horizontal and vertical playing. Strive to be as musical as possible.

Now repeat this exercise but use the A string as a pedal tone. Repeat this exercise again, but this time use a low D as the pedal tone (drop your low E string a step.) Now tune the low E string up to an F and repeat the exercise yet again. Now drop low E to an E flat and so on. Keep going with this exercise until you cover all 12 keys. If you're worried about breaking low E strings, make a recording of the 12 pedal tones. Make each pedal tone last for about 4 minutes. The important thing is that you play and you explore and you learn. It should be a joy. Good luck and make some music.